The bell curve – an example
Today’s lecture is a minimal introduction to the normal distribution – often called the “bell curve” – and will be based around a simple example. Prerequisites are only the ability to add integers, and an open mind.
The lecture is given by Dr. Venstad, who has previously also taught various advanced applied mathematics courses (computational physics, algorithms and datastructures, etc.) at the Norwegian University of Science and Technology.
The normal distribution – what and why?
The normal distribution has its name because it is just that – a very normal distribution. It is typically the result of adding many indenpendently random variables, which is a surprisingly common both in physics and mathematics.
As an example, consider tossing a coin an even number of times: every time it lands heads up, you score one point, and every time it lands tails up, you lose one point. Your final score, after 2N tosses, is then a prime example of something that follows the normal distribution; the most likely score is … take a guess! … 0! Even so, with many throws, the chances of scoring exaclty 0, are minute. Scoring 1 is impossible, but scoring 2 is almost as likely as scoring 0. Scoring 4 is slightly less likely again, and so on, with increasing skew. The least likely result is a score of plus or minus 2N. It is, perhaps, not obvious why different scores have different likelihoods, but this is so simply because scoring, say, 2N, requires you to toss heads every time, while scoring 0 can be done in any number of ways, as long as the number of heads and tails are equal. Thus there are many more ways of scoring 0, each as likely as the other, or as likely as scoring 2N, and the total chance of scoring 0 is the sum of the chances for each of these. Shown below is the probability for scoring each of the possible results when performing 32 tosses.
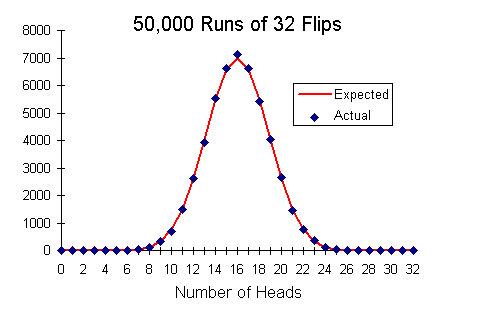
Because of its shape, the graph of the normal distribution is often called “the bell curve”.
A simple example – taking an accurate shot.
Consider someone aiming to take a shot. They are aiming at a specific point; alas, various disturbances contribute random inaccuracy to the shot: the miniscule movement of each of hundreds of muscles in the body of the shooter, gusts of wind blowing in different directions at different points along the trajectory of the projectile, etc… The sum is inaccuracy in the horizontal, as well as the vertical, direction. One of the pleasant properties of the normal distribution is that smearing the initial point aimed at first in the x-direction, according to a normal distribution, and then in the y-direction, according to the same normal distribution, results in a two-dimensional distribution which is perfectly rotationally symmetric, like shown below. (A “Gaussian distribution” is yet another name.)
To make it feasible to do any computation by hand, we need to discretise this distribution. Let’s go with a grid as shown below. The point the shooter is aiming at is at the centre of the three green hexes.

Now let’s assign a range of numbers to each cell, such that we can simulate a shot simply by drawing a random number and checking which cell has that number contained in its range. The size of the range in each cell is then proportial to the probability of hitting that cell. Below is the same grid with ranges assigned such that the probability of hitting each cell matches the normal distribution shown two images earlier, more or less.

Although this grid is certainly crude, compared to the blurry one shown above, it still has roughly the same density distribution. Note that there is nothing outside the red cells; this is the same as saying no shot will ever land outside of those – a truncation of the normal distribution.
Time for excercises!
The answer to each exercise is shown on the line below, but is blurred; click to sharpen it.
Exercise 1a: What is the probability of hitting the upper green cell?
It contains 10 out of 123 numbers, so 10/123.
Exercise 1b: What is the probability of hitting any green cell?
The union of the ranges in the green cells has size 30, so 30/123.
Good. Let’s call the green shots highly accurate, as they are, after all, closest to the centre of aim. Now let’s examine the probability of taking a highly _in_accurate shot, i.e., hitting a red cell:
Exercise 2a: What is the probability of hitting the upper red cell?
It contains 2 out of 123 numbers, so 2/123.
Exercise 2b: What is the probability of hitting any red cell?
The union of the ranges in the red cells has size 30, so 30/123 again.
What, highly accurate and highly inaccurate shots are equally likely? Cool, that’s exactly what we want! Also, it matches what is written in a certain, fabled, .pdf of knowledge, written by what is probably one of the elder gods.
So, highly accurate and highly inaccurate shots are equally likely, but this tome of ancient lore mentioned
that mediocre shots are actually the most likely, because of some “bell curve”. We have a bell curve now,
haven’t we, so let’s see if we can confirm this last piece of information, passed down by the gods, as well:
Exercise 3a: What is the probability of hitting the upper yellow cell?
It contains 7 out of 123 numbers, so 7/123.
Exercise 3b: What is the probability of hitting any yellow cell?
The union of the ranges in the yellow cells has size 63, so 63/123.
Yes, hitting a yellow cell, i.e., a cell which lies in the middle between the centre and the outer boundary, is really the most likely of all outcomes. Fantastic!
Finally, it should be easy to convince ourselves that half the shots will land on the outside of the imagined yellow circle whose radius is half that of the truncation boundary, i.e., the outside of the red cells. We already know green and red is equally likely, and this half-radius circle cuts the yellow cells right at the middle, so it’s fair to say this criterion is satisfied as well.
But we started out with a bell curve which was centred between the green hexes … what is this magic!?
The magic is simply that there are many more yellow cells than green ones, and so it is much more likely to hit a yellow cell, even though each green cell is more likely to hit than each yellow. No more, no less.
In all fairness …
There is also a second bell curve here, but it’s not found directly in the images above; rather, if we make a plot with accuracy along the x-axis and probability of taking a shot of a given accuracy along the y-axis, this plot contains the three points (high, 30/123), (medium, 63/123), (low, 30/123). This is also acceptable as a bell curve.
Furthermore, this is the curve we would get if we plotted the probability of taking a given shot as a function of radius, while collapsing the angle portion of the polar coordinates we alternatively could have used to express our grid.
It should be noted that while both these curves – a slice along the x-axis or the one with the radius – can be made simultaneously normal in this example, this is not true in the continuous case; however, they can always be made simultaneously close to normal, and so the fear that has pervaded this forum lately, of a ring of extreme likelihoot precisely at a certain yellow circle, should be no more than phantoms: if this implementation has indeed been chosen, it is clearly in error, and will be remedied. I think it has not. (Some will still claim this, based on experience. However, human experience and statistics do not blend well, as discussed in, e.g., this fantastic book.)
Concluding remarks.
What we have seen today is that it’s perfectly possible for each of the following statements to be simultaneously true:
- There is a bell curve with peak at the centre of aim.
- There is a bell curve with peak at mediocre accuracy, i.e., at the half-radius of the cut-off.
- Half our shots land inside the half-radius circle. (This circle may even be computed to fit this criterion?)
- Highly accurate and highly inaccurate shots are equally likely.
Thanks for reading, and I hope you learned something!
Respectful questions will be answered.

